Banned
I very much understand that there are many different ways to teach math well. I see other teachers sometimes and think, "WOW... but I could never do that." It's often a matter of personal style and most importantly, assessing and meeting the needs of your specific kids. Somewhere in all of that, however, are best practices that we (should) learn in ed school or from each other. In the same vein, there are many different ways to teach math poorly. Somewhere in all of that are what you might call anti-best practices, certain ways of teaching that do more to harm student learning than to support it. Besides all the "teacher moves" that don't work, there are some content-specific anti-best practices I've seen over the years that make me want to pull my hair out every time a kid mentions one.
The following is a list of phrases, algorithms, and "tricks" that I wish would be banned from every math class.
Cross Multiplication
Cheers to the genius who decided that it would really help kids to draw a big X through an equals sign and multiply the numbers on the ends. Yes, cross multiplication "works" in the case of a straight proportion with one unknown, but that's a very specific case. Kids like cross multiplication because it's easy to remember (although the dividing at the end gets confusing), but what they don't remember is when you should actually use it. Try this experiment if you have a middle schooler or high schooler handy: if they remember cross multiplication, then give them three problems, one where two fractions are set equal to each other, one where the fractions are added, and one where they are being multiplied. You'll be amazed at how many kids draw an X on all three problems. This is so common that my lesson on cross multiplication (and why you're not allowed to use it in my class unless you can explain to me why it works) is based on someone raising their hand and making this mistake. And it always happens. Kids don't understand why it works, so they don't know how or when to use it.
One of the biggest things I want my students to learn from my class is that math and math steps should always make sense. I teach them "fraction busters" which is essentially a long version of cross multiplication. Fraction busters involves multiplying by all the denominators in an equation in order to "bust" the fractions and get something more reasonable to work with. I push my kids to say that we're multiplying because fractions are division and we want to undo the division by doing it's opposite. If there's a reason behind their math steps (besides "It's what my old math teacher taught me") then there's a very good chance that they're doing something right, and an even better chance that they'll understand how to fix it if it's wrong.
Fun story: last year another math teacher and I literally sprinted across the school trying to find the algebra teacher to make sure he didn't teach cross multiplication. I like to think it was like a movie when Maura found him, that she busted through the door (no pun intended) and dove in slow-motion to knock the whiteboard marker out of his hand before he could draw an X through the equals sign.
"Cross Cancel"
Honestly, I don't even know what this means, but it always comes out of some kid's mouth when we're talking about fractions. I think it has something to do with multiplying and simplifying fractions? In any case, if I don't know what it means and kids can't explain it to me, it's obviously not helping them learn. It's just another "rule" that has no sense-making behind it, so kids mess it up.
FOIL
Oh, binomials, the way you torture Algebra I students is amazing. FOIL (first, outer, inner, last) is definitely the way I learned how to multiply binomials and definitely the way I continued to do it until a couple of years ago. Again, this is another "rule" that kids don't understand the reasons behind. It's a little harder to mis-apply than something like cross multiplication, but it's detrimental because it's extremely limiting. I was a good math student, and I definitely did not understand for a very long time how to multiply a binomial with a trinomial (let alone larger polynomials) because it didn't fit the FOIL pattern. Another significant issue is that because FOIL has no logic behind it, there's no logic to un-FOILing AKA factoring, which is consistently one of the most difficult topics in Algebra I.
The solution? The best way I've ever seen this taught--and what I continue to use--is an area model. Here are some examples:
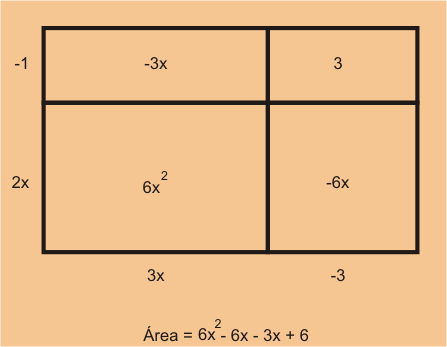 They make a lot more sense to kids, and work well for any kind of multiplication of polynomials because you can make the generic rectangles any size. They also make factoring unbelievably easier. Learning about generic rectangles was life-changing for my own mathematical understanding and for the way I teach algebra.
They make a lot more sense to kids, and work well for any kind of multiplication of polynomials because you can make the generic rectangles any size. They also make factoring unbelievably easier. Learning about generic rectangles was life-changing for my own mathematical understanding and for the way I teach algebra. "A negative and a negative is a positive"or "A negative and a positive is a negative."
What's the key word in these phrases? Oh, there isn't one because it's completely ambiguous. What does "and" mean? To make these "rules" correct, "and" should mean "multiplied or divided by" but of course kids don't remember that. You'd be amazed at how many kids think -5 + 10 is either -15 or -5. Multiplication of positive and negative numbers gets a little more complicated with regard to the sense-making aspect--can YOU explain why two -5 x -5 = +25? But the sense-making around adding positive and negative numbers is not difficult, so if we can at least start there hopefully there will be less confusion with multiplication/division.
a^2+b^2=c^2
No, I don't want to get rid of the Pythagorean Theorem. But who thought it was a good idea to name the sides of the triangle a, b, and c? How do those help, especially when it doesn't matter which of the legs is a and which is b? I got a semi-angry email from another math teacher this year asking why we'd teach it that way. The answer: I don't. I teach it by first looking at the geometric representation, so I want the kids to be able to verbalize something like, "The areas of the two smaller squares add to equal the area of the bigger square." Algebraically, I teach it as "Leg^2+Leg^2=Hypotenuse^2".
"Cancel out"
Another terribly ambiguous phrase. Kids love crossing things out (who doesn't? It feels so satisfying), so they love saying that things cancel. But "canceling" is another word that means nothing, at least when it comes to sense-making and giving reasons. We teach that adding and subtracting from both sides of an equation is "making zeros." Simplifying a fraction is "making ones." Squaring and square roots "undo each other." Because that's exactly what's happening. Math isn't magic, so numbers and symbols shouldn't just vanish with no explanation. If kids can make sense of these very fundamental identities, they're set up to understand all kinds of algebraic manipulation and solving, as well as new operations and their inverses. And kids still get to cross stuff out.
There are two main ideas behind this post:
1. For kids to effectively learn math, it has to make sense. Seemingly arbitrary rules do not help them make sense of anything and only serve to deepen their belief that math is some confusing, magical subject that's only accessible to a select few.
2. Unlearning a misconception is exponentially more difficult than learning something right in the first place. And what's tricky is that misconceptions are often applied in a way that gets a correct answer. So kids who I meet in 9th grade who have been cross multiplying for 2-3 years get frustrated because they've been able to solve all these proportions correctly, not realizing that the other ways they've been applying it are where the real problem is.
I'm not completely innocent regarding all the anti-best practice above. I did teach things that way or would have taught them if I'd never seen an alternative. It makes me wonder what else I'm doing wrong that's driving upper-level teachers crazy...


1 comment:
Bravo! I want to share this with every math teacher I know--from K up. I know those "rules" you give, but for many of them I still don't understand what they mean, which may explain some of the fatal errors I make in math and surely explains the many times I simply throw up my hands in dispair.
Post a Comment