The American Dream
Conversation with three white students:
The State of California has licensed me to hold the future in my hands.
Conversation with three white students:
Labels: California, Teaching, USA
A couple weeks ago (5 weeks to be exact) I was reading this post from the Freakonomics blog. I'm fascinated by the idea of what motivates people, for myself, for my students, and just for my interactions with other people. The post discusses "commitment contracts," which I make in my mind all the time: cooking dinner more often, going to bed at a reasonable hour, eating healthier, not checking work email after a certain time and all those other things that I know will make my life better. But of course, I'm not great at following through on any of it. It's easier to pick up takeout, stay up a little later, have a bowl of ice cream, and double-check that no school emergency has come up since I last looked. When it comes to things that impact only me, I need more motivation.
Stickk.com, a website set up by researchers from the Yale School of Management, turned out to be exactly what I needed. The way it works is that you set up a commitment contract with yourself about anything. I chose going to the gym at least four times a week and decided I'd start out with a 5-week commitment. They send you an email every week asking whether you met your commitment and keep track of how you're doing. For me, just putting it in writing is not enough, so StickK adds another dimension. I gave them my credit card number and if I didn't make it to the gym four times in a given week, StickK.com would charge me $25 (you set your own price point; I started on the lower end in case this experiment completely failed).
Just to raise the stakes a little bit more, StickK gives you the option of where your money goes. It can be to another person of your choice, but I felt like most of my friends would feel uncomfortable enough with the arrangement that they'd either decline to participate or would spend the money on us doing something fun together. Another option is to give your money to charity, but I'd feel okay if I skipped out on the gym and the United Way got $25. So StickK has a third option: the anti-charity. I set up my contract so that if I didn't meet my commitment, not only would I lose $25, it would go to the Institute for Marriage and Public Policy. You can probably guess by the name that this organization defines marriage under very specific, very exclusionary terms. Not exactly a cause I want to support. (There are anti-charities for all sorts of beliefs; I love that the list of options includes a bunch of different British football clubs.)
I'm amazed at how well this commitment contract worked for me, and I'm proud to say that for the past five weeks I've gone to the gym at least four times a week. The money and the anti-charity have unquestionably been the major motivating factor. There were multiple days when I dragged myself off the couch or forced myself to stop on the way home from school because I was so horrified at the thought of donating to an anti-gay marriage organization. This is a very busy, very difficult time of year and I know there are a number of days when I would have skipped out if this threat weren't looming over my head.
Now this post just sounds like an advertisement for stickK.com and maybe it is. Seriously, I can't wait to try out some other commitments to see what I can do when I force myself into it.
PS - A fun thing to do is check out the homepage where they show a list of commitments that other people are making. There are a lot of the usual like save money, lose weight, eat healthy, etc., but there are also some amazing ones: "make $1 million by a certain age," "be more awesome," and "be nice to my girlfriend." I am so fascinated by other people.
Labels: California, News, USA
I very much understand that there are many different ways to teach math well. I see other teachers sometimes and think, "WOW... but I could never do that." It's often a matter of personal style and most importantly, assessing and meeting the needs of your specific kids. Somewhere in all of that, however, are best practices that we (should) learn in ed school or from each other. In the same vein, there are many different ways to teach math poorly. Somewhere in all of that are what you might call anti-best practices, certain ways of teaching that do more to harm student learning than to support it. Besides all the "teacher moves" that don't work, there are some content-specific anti-best practices I've seen over the years that make me want to pull my hair out every time a kid mentions one.
The following is a list of phrases, algorithms, and "tricks" that I wish would be banned from every math class.
Cross Multiplication
Cheers to the genius who decided that it would really help kids to draw a big X through an equals sign and multiply the numbers on the ends. Yes, cross multiplication "works" in the case of a straight proportion with one unknown, but that's a very specific case. Kids like cross multiplication because it's easy to remember (although the dividing at the end gets confusing), but what they don't remember is when you should actually use it. Try this experiment if you have a middle schooler or high schooler handy: if they remember cross multiplication, then give them three problems, one where two fractions are set equal to each other, one where the fractions are added, and one where they are being multiplied. You'll be amazed at how many kids draw an X on all three problems. This is so common that my lesson on cross multiplication (and why you're not allowed to use it in my class unless you can explain to me why it works) is based on someone raising their hand and making this mistake. And it always happens. Kids don't understand why it works, so they don't know how or when to use it.
One of the biggest things I want my students to learn from my class is that math and math steps should always make sense. I teach them "fraction busters" which is essentially a long version of cross multiplication. Fraction busters involves multiplying by all the denominators in an equation in order to "bust" the fractions and get something more reasonable to work with. I push my kids to say that we're multiplying because fractions are division and we want to undo the division by doing it's opposite. If there's a reason behind their math steps (besides "It's what my old math teacher taught me") then there's a very good chance that they're doing something right, and an even better chance that they'll understand how to fix it if it's wrong.
Fun story: last year another math teacher and I literally sprinted across the school trying to find the algebra teacher to make sure he didn't teach cross multiplication. I like to think it was like a movie when Maura found him, that she busted through the door (no pun intended) and dove in slow-motion to knock the whiteboard marker out of his hand before he could draw an X through the equals sign.
"Cross Cancel"
Honestly, I don't even know what this means, but it always comes out of some kid's mouth when we're talking about fractions. I think it has something to do with multiplying and simplifying fractions? In any case, if I don't know what it means and kids can't explain it to me, it's obviously not helping them learn. It's just another "rule" that has no sense-making behind it, so kids mess it up.
FOIL
Oh, binomials, the way you torture Algebra I students is amazing. FOIL (first, outer, inner, last) is definitely the way I learned how to multiply binomials and definitely the way I continued to do it until a couple of years ago. Again, this is another "rule" that kids don't understand the reasons behind. It's a little harder to mis-apply than something like cross multiplication, but it's detrimental because it's extremely limiting. I was a good math student, and I definitely did not understand for a very long time how to multiply a binomial with a trinomial (let alone larger polynomials) because it didn't fit the FOIL pattern. Another significant issue is that because FOIL has no logic behind it, there's no logic to un-FOILing AKA factoring, which is consistently one of the most difficult topics in Algebra I.
The solution? The best way I've ever seen this taught--and what I continue to use--is an area model. Here are some examples:
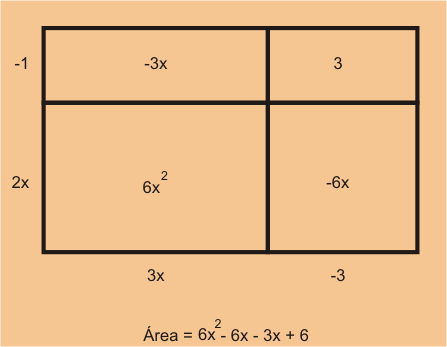 They make a lot more sense to kids, and work well for any kind of multiplication of polynomials because you can make the generic rectangles any size. They also make factoring unbelievably easier. Learning about generic rectangles was life-changing for my own mathematical understanding and for the way I teach algebra.
They make a lot more sense to kids, and work well for any kind of multiplication of polynomials because you can make the generic rectangles any size. They also make factoring unbelievably easier. Learning about generic rectangles was life-changing for my own mathematical understanding and for the way I teach algebra. Labels: California, Math, Teaching, USA
Pictures, as promised. First, crazy hair day. It's hard to see well in these pictures, but my quasi-mohawk/stegosaurus impersonation was quite the hit. The flowers were a last-minute addition in the morning that I'm glad to have made. There were only two problems: first, by the end of the day I had a terrible headache, which I eventually realized was from having my hair pulled so tightly for 9 hours. Second, I had to meet with a parent in the afternoon, which I was prepared for by choosing a hairstyle that could be undone (unlike my colleague Lisa, as you can see below). But in all the rush of after-school meetings, there was no time to turn myself into someone who you'd trust with your child so the whole meeting was kind of awkward. I hope that the kid explained to his mom that his teachers don't usually look like that.

Labels: California, Holidays, Pictures, Teaching, USA